高中数学：鸡爪定理（三）

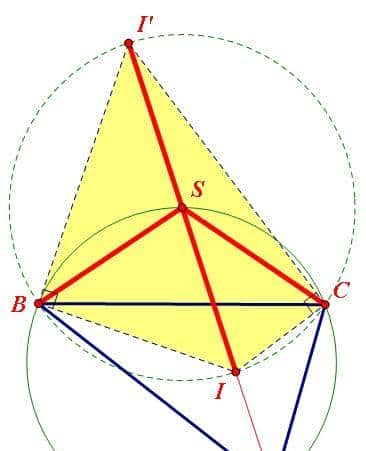
再回顾一下鸡爪定理内容：设I和I'分别是△ABC的内心和A旁心，则SI＝SB＝SC=SI'。

前面两篇文章分别介绍了鸡爪定理的最新应用和经典问题，但是这只是冰山一角，本人天资有限，但是耐性尚好，知无不言言无不尽，喜爱咬定青山不放松，不贪多求全，希望能把一个问题讲透彻，今天继续介绍鸡爪定理在重大赛事（如高中数学联赛、中国数学奥林匹克（CMO）、中国国家队选拔考试（TST）、国际数学奥林匹克（IMO）等）中的应用。

1、 如图，设△ABC外接圆O半径为R，内心为I，∠B=60°,∠A<∠C,∠A外角平分线交圆O于E。

证明：（1）IA=AE,

(2) 2R<IO+IA+IC<(1+√(3))R

（1994年高中数学联赛）

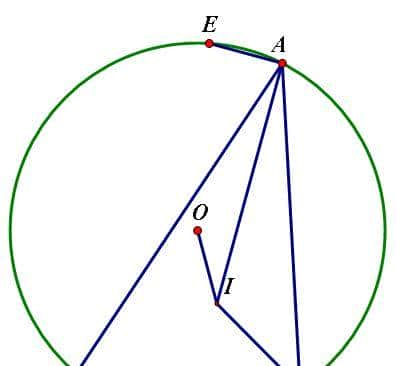
证明：

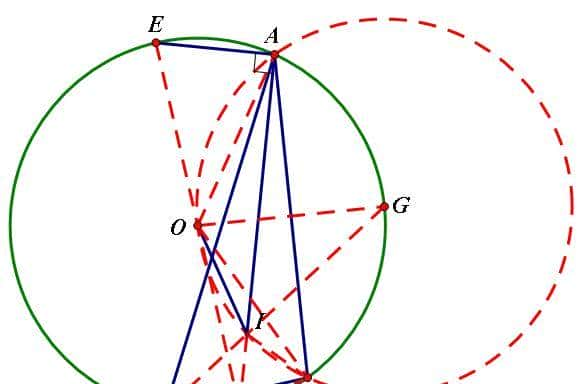
(1)如图，设BI、AI交圆O于G、D，显然EOD共线，

则∠AIC=90°+∠B/2=120°=2∠B=∠AOC,

由正弦定理GA=2Rsin30°=R

结合鸡爪定理得A,O,I,C在以G为圆心R为半径的圆上；

则∠AOE=2∠OAD=∠OGI,

故△AOE≅△OGI(SAS),则IO=AE,

(2) 由鸡爪定理有IC=ID，又IA=AE,

则在△AED中，有AE+IA+ID>DE,

即IO+IA+IC>2R,

A/2=θ,0<θ<30°,

∠AED=60°+θ

IO+IA+IC=2R(sin(60°+θ)+cos(60°+θ))

=2√(2)Rsin(105°+θ),

为θ单调递减函数，θ=0时，为(1+√(3))R

综上 2R<IO+IA+IC<(1+√(3))R

注：

1、）本题另一种观察角度是含有一个60°角的三角形，这类三角形性质超级丰富，竞赛中也常常出现，后面有空了我会专门开辟一个专题讲解此类问题，在此先挖个坑，立个flag。

2、）本题第二问最后用了一些三角计算，虽然我叹服于几何之美，但是并不是说就不能使用几何以外的证题方法，纯几何思路受阻，马上就要调整思路，适当计算，毕竟计算才是王道！好多几何构型的核心就是一些代数恒等式。

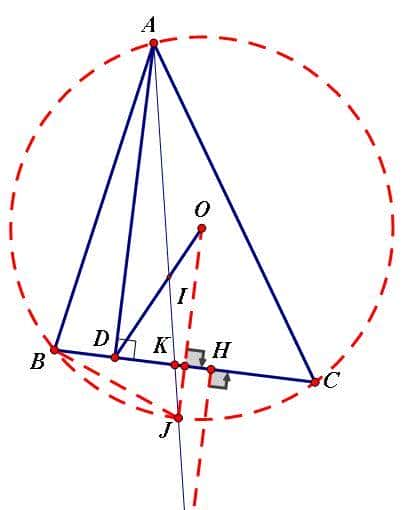
2、如图，O、I分别为△ABC的外心和内心，AD是BC边上的高，I在线段OD上。

求证：△ABC的外接圆半径等于BC边上的旁切圆半径。（1998年高中数学联赛）

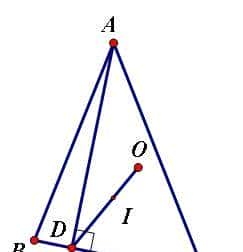
证明：（为了真实反映我的思考过程，我使用分析法）

如图，设旁心为I'，则A,I,I'共线，设I'H⊥BC,显然OJ⊥BC,

由鸡爪定理得JI=JB=JI',

OJ=I'H<=>OJ:AD=I'H:AD

<=>JI:IA=I'K:AK

<=>JI:IA=I'K:AK=(I'K-JI):(AK-AI)=JK:KI(等比定理)

<=>JI:(IA+JI)=JK:(KI+JK)(等比定理)

<=>JI:JA=JK:IJ

最后这个显然是鸡爪定理的基本性质，从而原结论成立。

注：

1、)对于本题我是记忆犹新，或者说是刻骨铭心，由于我就是98年参与的高中联赛，虽然之前做了许多准备，但是当年的二试三个题目都超级难，我只把这个第一题通过复杂的三角计算算了出来，最后只是获得了陕西省一等奖，分数大致是十来名，但是当时陕西省只有三个参与冬令营的名额，我的高中竞赛就此止步了。所以此题比较容易想到的方法是三角计算，就是过程稍微复杂一点。

2、)本文第一段提到质疑的重大性，下面再说一件真实的事情说明质疑的好处。当年陕西获得进冬令营的三名同学后来都成了我的大学同学，其中一个同学穆鹏程说了他进省队的缘由——他质疑此题是错题！由于显然当三角形为等腰三角形时OID共线恒成立，此时不必定有其旁切圆半径等于外接圆半径。后来改卷组经过多次磋商和请示，认为此解答正确！我觉得判卷的结果超级合理，对这种敢于质疑的学生必须加以褒奖！这种学生必定前途无量。（目前他好像已经是大学教授）所以本题严格上讲应该再加上非等腰的条件。

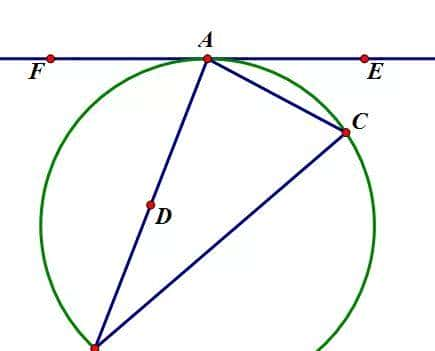
3、如图，在△ABC中，设AB＞AC，过点A作△ABC的外接圆的切线l，又以点A为圆心，AC为半径作圆分别交线段AB于点D；交直线l于点E、F．

证明：直线DE、DF分别通过△ABC的内心与一个旁心．（2005年高中数学联赛）

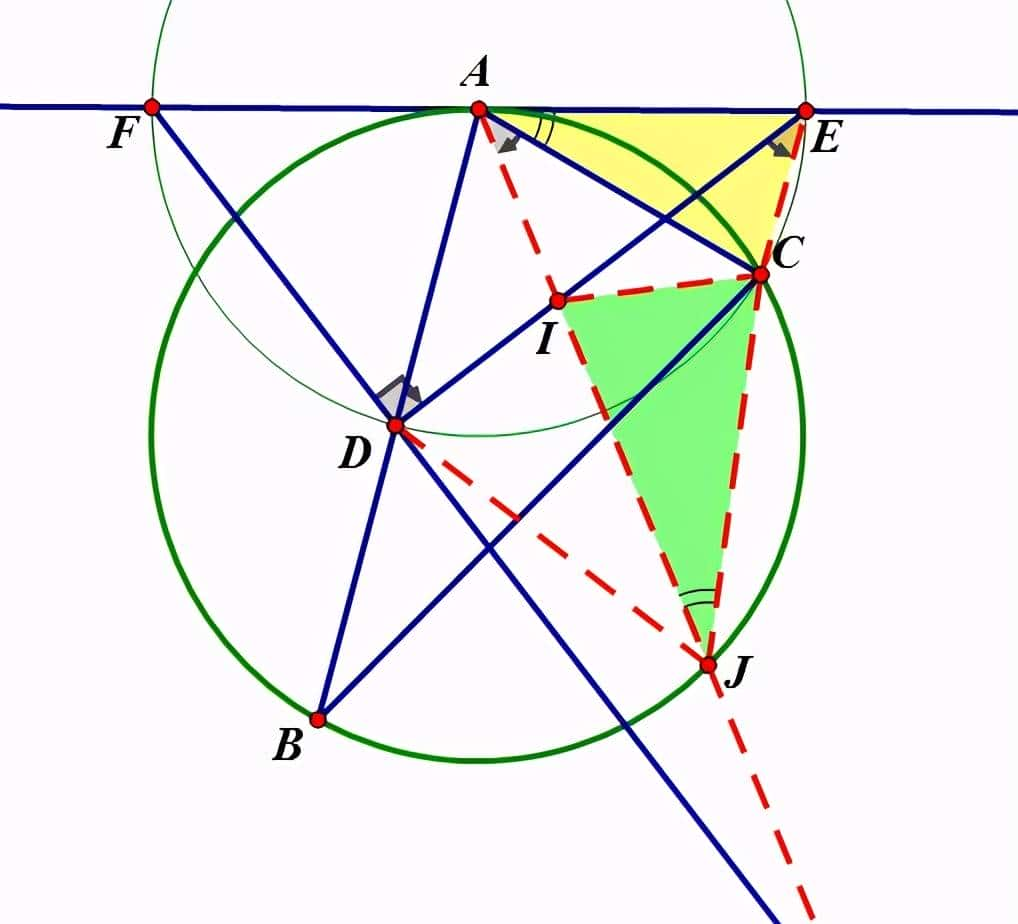
证明：

设∠BAC内角平分线交DE、DF于I、I'，

则∠CAI=1/2∠BAC=∠DEC,

故AICE共圆,

∠JIC=∠AEC；

又∠EAC=∠IJC,

故∠JCI=∠ACE=∠AEC=∠JIC,

即JI=JC,

由鸡爪定理逆定理知I为△ABC的内心；

又ID=IC,AD=AC，则AIJ为CD中垂线，

故JD=JI=JC

又ID⊥DI'，故JI=JI'，从而I'为△ABC的内心；

综上结论成立。

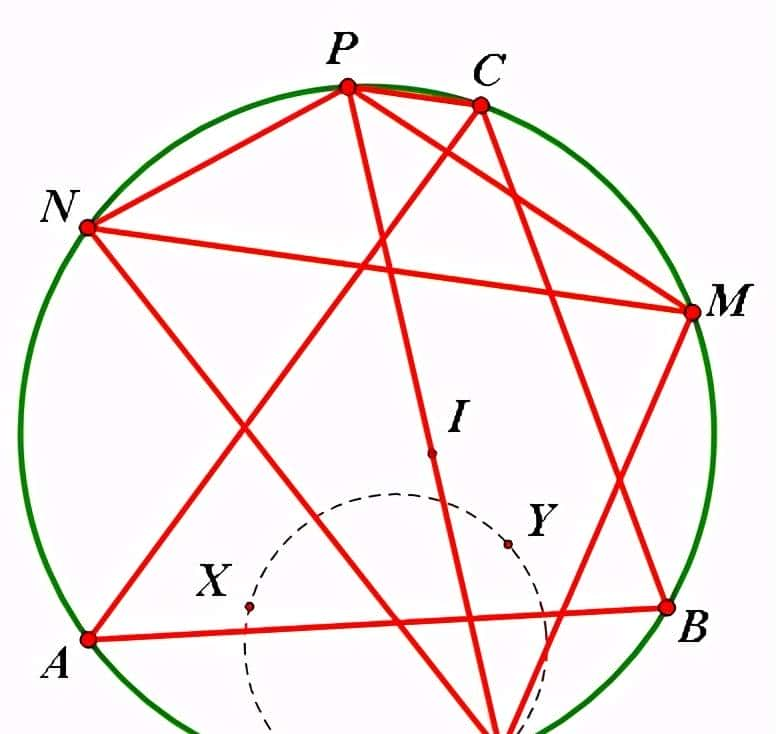
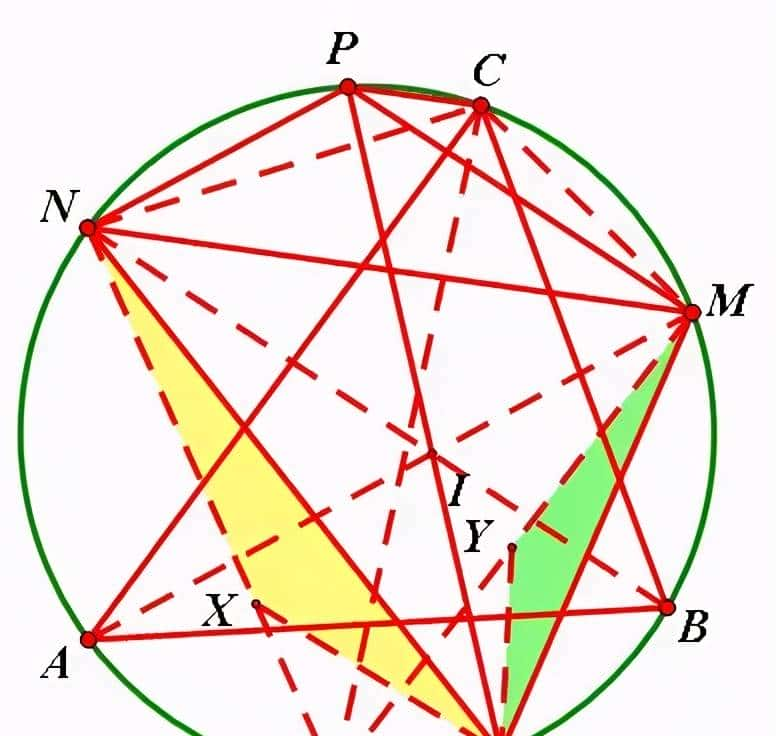
4、如图M,N分别为锐角三角形ABC的外接圆O上弧 BC、AC 的中点．过点C 作CP//MN 交圆O于 P点， I为△ABC的内心，连接PI并延长交圆O于T ．

⑴求证：MP*MT=NP* NT；

⑵在弧AB（不含点C）上任取一个异于A,B,T的点 Q，记△AQC ,△BQC 的内心分别为X,Y

求证： QTXY四点共圆．（2009年高中数学联赛）

证明：

(1)依题意NIB,AIM共线，

由CP//MN 得CPNM为等腰梯形，

结合鸡爪定理得NI=NC=PM,MI=MC=PN,

故NIMP为平行四边形，则PI平分NM，

故△NPT与△MPT面积相等，

故MP*MT=NP* NT；

(2)依题意NXQ,QYM共线，

由鸡爪定理得NX=NC=PM,MY=MC=PN,

再结合(1)即得NX:MY=TN:TM,

又∠QNT=∠QMT,

故△TXN∼△TYM,

则∠QXT=∠QYT,则QTXY四点共圆．

注：

1）本题图形略复杂，大有乱花渐欲迷人眼之感，但是只要抓住内心的核心性质——鸡爪定理，思路并不难想到。第二问中的类似也是由共圆自然分析出来的。

2）本题中T点实际上就是曼海姆定理中伪内切圆与外接圆的切点，这也算是曼海姆定理构型中的性质，里面还有许多“宝藏”值得挖掘。

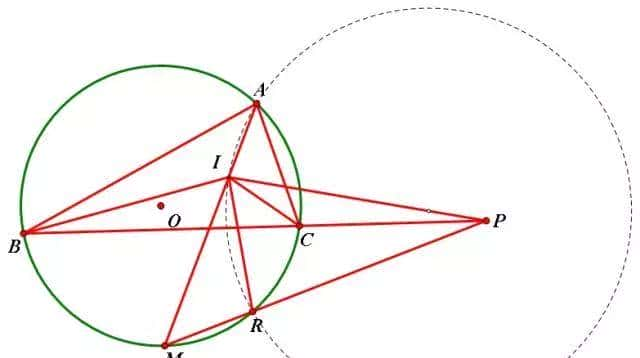
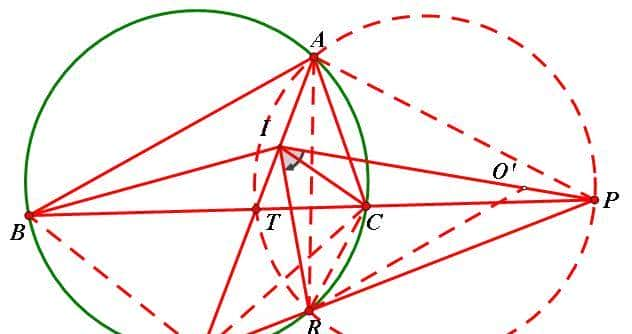
5、已知：如图，I为△ABC内心，AI交外接圆O于M，BIC外角平分线交BC于P，MP交圆O于R，

求证：△AIR外心在IP上（20170619 我们爱几何问题 作者：赵斌）

证明：

设△AIR外心为O’，△ABC角为A,B,C，

由鸡爪定理知(MI^2)=MB(^2)=MT*MA=MR*MP,

则ATRP共圆，则

∠RIP=∠MIP-∠MIR=∠MIC+∠CIP-∠RPI

=∠MCI+∠CIP-∠RPC-∠CPI

=∠MCB+∠ICB+∠CIP-∠RAI-∠CPI

=∠MCB+2∠CIP-∠RAI=(A/2)+(B+C)/2-∠RAI

=90°-∠RAI=90°-(∠RO’I/2)=∠RIO’

即O’在IP上

注：

此题为第一篇鸡爪定理的最后思考题，如果对这个构型比较熟悉，这个题目还是比较简单的。

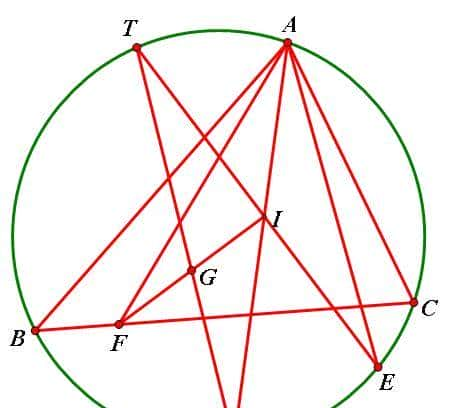
6、设△ABC内心为I，外接圆为O，AI交圆O于D，E为弧BDC上一点，F为BC上一点，且∠BAF=∠CAE<∠BAD,G是IF中点。

求证：DG与EI交点在圆O上；（2010年第50届IMO）

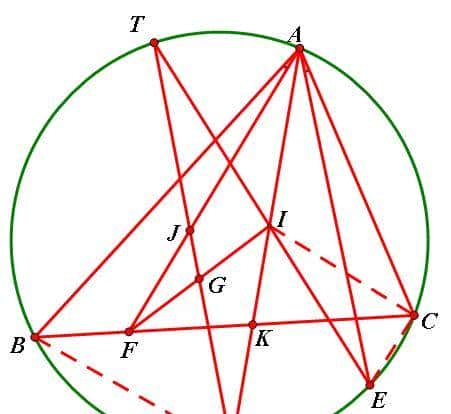
分析证明：

证明结果有些模糊，中点很难用，

由图形的唯一性，设EI交圆O于T，

我们等价于证明TD平分IF，

由梅涅劳斯定理等价于证明(AD:ID)(IG:GF)(FJ:JA)=1

即证明AD:DI=AJ:JF，

即证明AD:(DI+AD)=AJ:AF;

由已知显然△ABF∼△AEC,故AF:AC=AB:AE,

同理△AJD∼△AIE,故AJ:AI=AD:AE,

两式相除得AJ:AF=(AD:AB)(AI:AC);

从而只需证明：AD:(DI+AD)=(AD:AB)(AI:AC)，

即证明：AB:(DI+AD)=AI:AC;

至此基本结束，由于结果已经与E、F无关！

由角平分线定理有AI:AC=KI:CK=AK:(AC+CK)

又△ACK∼△ADB,故AK:(AC+CK)=AB:(DB+AD),

由鸡爪定理DI=DB，

从而结论成立！

最后说一下，本篇文章里面的题目都很经典，许多同学可能都反复刷过，但是正如单墫单老所言：好的音乐，不妨多听几遍；好的题目，不妨多做几遍。提议大家重新思考一下做过的题目，必定会有新的收获。温故而知新，温故必知新。甚至还要学新以温故，我们学习新题的时候如果能联想到做过的其他题目，必定要及时回顾、对比、提升，这样对新的问题和老的问题都会有深刻的印象和理解。这也是我学习中的一点经验体会，希望能对大家有协助。