基本信息
发表刊物
NeurIPS 2025
作者信息
Yisong Fu1,2、Zezhi Shao1、 Chengqing Yu1、 Yujie Li1,2、 Zhulin An1,2、
Qi Wang3、 Yongjun Xu1,2∗、Fei Wang1,2∗
1 中国科学院计算技术研究所人工智能安全国家重点实验室
2 中国科学院大学
3 清华大学自动化系
解决的问题
Motivation
深度时间序列预测（Deep Time Series Forecasting, TSF）模型存在严重的过拟合问题。
问题根源： 时间序列数据本身对 噪声（noise）和异常值（anomalies）具有固有的脆弱性。
现有范式缺陷： 当前流行的深度学习范式是统一优化所有时间步，通过均方误差（MSE）损失函数来学习。这种做法会导致模型不加区分地学习那些 不确定或异常（uncertain and anomalous）的时间步，最终导致模型性能下降和过拟合。
解决方案
论文提出了一个新颖的选择性学习（selective learning）策略作为其核心灵感和解决方案。
核心思想： 选择性学习通过筛选整个时间步的一个子集来计算优化过程中的 MSE 损失。
目标： 这一策略旨在引导模型 专注于具有泛化能力（generalizable）的时间步，同时忽略不具有泛化能力（non-generalizable）的时间步。
具体实现机制： 论文的框架引入了一个 双重掩码机制（dual-mask mechanism）来实现对目标时间步的选择。
提出的方法
Preliminaries
符号定义 (Notations)
| 符号 | 含义 | 维度 |
 |
多变量时间序列在时刻 t 的值。 | ($mathbf{R}^N$) ( N 个变量) |
| N | 时间序列中变量（特征）的数量。 | 标量 |
| L | 回顾窗口（Lookback Window Size）的大小，即用于预测的历史数据长度。 | 标量 |
 |
输入序列，即从 t-L 时刻到 t-1 时刻的历史数据。 | ($mathbf{R}^{L imes N}$) |
| F | 预测窗口（Forecasting Window Size）的大小，即需要预测的未来时间步数量。 | 标量 |
 |
预测序列，即模型预测的从 t 时刻到 t+F-1 时刻的未来值。 | ($mathbf{R}^{F imes N}$) |
|
真实序列（Ground Truth），即需要预测的真实未来值。 | ($mathbf{R}^{F imes N}$) |
| ($mathcal{D}_{ ext{train}}$) | 训练数据集，通过步长为 1 的滑动窗口方法从历史序列  中构建。 |
样本集 |
总结： TSF 任务就是给定过去 L 个时间步 (mathbf{X}_{t-L:t})，预测未来 F 个时间步 。
问题阐述 (Problem Statement)
当前深度学习（DL）解决 TSF 任务的标准范式。
A. 预测函数
深度学习范式在于找到最佳映射函数 
，它将历史输入 映射到预测输出 ：
($hat{mathbf{X}}_{t:t+F} = f(mathbf{X}_{t-L:t}; heta)$)
是一个由参数 
定义的深度神经网络。
B. 损失函数 (MSE)
为了优化模型参数 ，通常使用 均方误差 作为损失函数 ($mathcal{L}_{ ext{MSE}}$)：
目标： ($mathcal{L}_{ ext{MSE}}$) 衡量了预测值 （记为 ($f(mathbf{X}_{t-L:t}; heta)_i$)）与真实值 （记为 ($mathbf{X}_{t+i}$)）之间的差异。
关键点： 这个损失函数对预测窗口 F 内的所有 F 个未来时间步以及所有 N 个变量都进行了平均和统一优化。
C. 参数更新
模型参数 通过梯度下降（或其变体，如 Adam）进行迭代更新：
是训练的迭代次数（Iteration index）。
($eta$) 是学习率（Learning Rate）。
正是这种 “ 统一优化所有时间步”（即公式 (1) ($mathcal{L}_{ ext{MSE}}$) 的求和项）的做法，使得模型在面对时间序列中的噪声和异常值时容易过拟合。
Selective Learning
Overview of Selective Learning
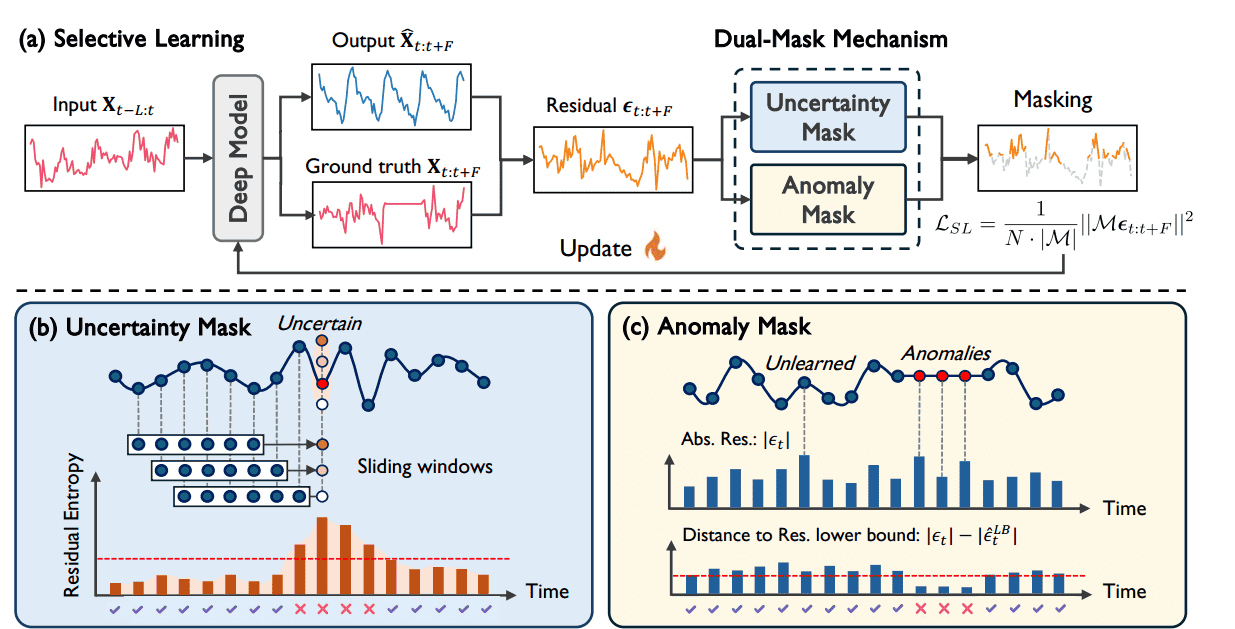
核心思想与动机
核心思想： 选择性学习是一种模型无关（model-agnostic）的训练策略，其主旨是仅在时间步的一个子集上计算 MSE 损失。
目标： 引导模型 选择性地关注可泛化（generalizable）的时间步，同时忽略不可泛化（non-generalizable）的时间步，从而解决过拟合问题。
不可泛化的两类时间步
有两种关键类型的不可泛化时间步会损害模型的泛化能力：
不确定时间步 (Uncertain Timesteps)：
来源： 主要来自时间序列中固有的噪声（noise）
特点： 具有高预测不确定性（high predictive uncertainty）
危害： 这些时间步的梯度更新方向是随机的，导致模型不必要地拟合噪声。
异常时间步 (Anomalous Timesteps)：
来源： 主要来自外生的异常事件（exceptional events），如传感器故障
特点： 预测残差（误差）显著大，即使模型的预测可能很“自信”（Confident）
危害： 强制模型通过 有偏的梯度更新（biased gradient updates）学习特定于实例的特征，损害泛化能力。
选择性损失函数的数学形式
为动态过滤掉这些不可泛化时间步，论文提出双重掩码机制，选择性学习损失函数 
定义为：($mathcal{L}_{ ext{SL}}( heta) = frac{1}{N cdot |mathbf{M}^{( au)}|} sum_{i=0}^{F-1} ||mathbf{M}^{( au)} odot (mathbf{X}_{t+i} – f(mathbf{X}_{t-L:t}; heta)_i)||^2 quad ext{(3)}$)
是在第 次迭代时生成的最终掩码。
($odot$) 表示逐元素乘法（在公式中，它实际上作用于残差，将被选择的时间步的残差保留，将未被选择的时间步的残差置零）。
是掩码中 ($1$) 的个数，用于归一化。
掩码的构成： 最终的掩码 
是由不确定性掩码($mathbf{M}_u^{( au)}$) 和异常掩码 
通过元素级 OR 运算 (($vee$) ) 得到的：
Uncertainty Mask
旨在识别具有高 预测不确定性的时间步，并提出一种基于 熵（Entropy-based）的掩码方法。
基于熵的不确定性度量
残差定义：(epsilon_t = mathbf{X}_t – hat{mathbf{X}}_t) ，表示在时刻 t 观测值 与预测值 
之间的残差（Residual）。
度量方式： 采用残差 ($epsilon_t$) 的微分熵（Differential Entropy） 
来量化预测的不确定性。
($H(epsilon_t) = int p(epsilon_t) ln p(epsilon_t) dt quad (5)$)
核心思想： 熵是衡量随机变量不确定性或信息量的指标。熵值越高，残差分布越分散（方差越大），表明预测的不确定性越高。
实践中的残差分布估计
由于时间序列数据是通过 滑动窗口（sliding window）构建训练样本的，一个给定的时间步 
在一个训练周期（epoch）中会被包含在多个输入窗口中，因此会被预测 ($n_t$) 次。
预测次数 
：($n_t = min{t – L + 1, F}$)。
L 是回顾窗口大小，F 是预测窗口大小。这个公式确保了我们只考虑该时间步在训练集 
范围内被预测的次数。
残差估计： 利用这最近的 次预测残差 (${epsilon_t^{(1)}, epsilon_t^{(2)}, cdots, epsilon_t^{(n_t)}}$) 来估计残差的分布 
的参数 ($psi$) 。
($hat{H}(epsilon_t) = int l(hat{psi}|epsilon_t) ln l(hat{psi}|epsilon_t) dt quad ext{(7)}$)
高斯假设下的简化计算
为了在实践中简化计算，作出了残差 ($epsilon_t$) 服从高斯分布的假设：
。
方差估计： 在高斯假设下，不确定性（熵）与残差的方差 ($hat{sigma}_t^2$) 直接相关。方差通过历史残差样本估计得到：
其中 ($ar{epsilon}_t$) 是 ($n_t$) 个残差的平均值。
熵估计： 高斯分布的微分熵公式为：
注意： 由于 ($frac{1}{2} ln(2pi e)$) 是常数，熵 
实际上与方差 ($hat{sigma}^2_t$) 是单调递增关系。因此，高不确定性等价于高方差。
理论保障 (Theorem 1)
一个关键的挑战是：用来估计 
的 ($n_t$) 个残差 (epsilon_t^{(i)}) 是在不同的训练迭代 下，由不同参数 
的模型 ($f(cdot, heta^ au)$) 产生的。这可能导致方差估计不准确。
定理 1（方差估计误差的上界）： 在不同参数下估计的方差 ($hat{sigma}^2_t$) 与在同一参数下估计的方差 
之间的误差上界：
($|hat{sigma}^2_t – hat{sigma}^2_t( heta^ au)| leq 4L_f R eta G (2K – 1) quad (10)$)
K 是每 epoch 的迭代次数。
是常量。
($eta$) 是学习率。
结论： 根据定理 1，通过选择足够小的学习率 (eta) 和足够大的批次大小（这隐含在 K 中），可以有效地控制这种由参数变化引起的估计误差，从而保证方差（以及熵）估计的有效性。
不确定性掩码的生成
最终的 ($mathbf{M}_u^{( au)}$) 掩码通过一个硬阈值（hard thresholding）策略生成：
阈值 
： 设定一个阈值 (gamma_u) （通常是基于顶部 
的残差熵确定的）。
掩码规则：
($(mathbf{M}_u^{( au)})_t = egin{cases} 0, & hat{H}(epsilon_t) > gamma_u quad ( ext{high-uncertainty}) \ 1, & ext{otherwise} quad ( ext{low-uncertainty}) end{cases} quad (11)$)
结果： 被标记为 0 的时间步被认为是不可泛化的（过于嘈杂），它们将被排除在损失计算之外，从而防止模型拟合噪声。被标记为 1 的时间步被选中参与优化。
Anomaly Mask
异常掩码（Anomaly Mask）的构建，其目标是识别和过滤掉由异常事件引起、具有显著大残差但泛化能力差的时间步。
朴素方法的局限性与挑战
朴素方法： 最直观的方法是直接过滤掉残差
较大的时间步。
局限性： 这种方法会不加区分地排除两类时间步：
真正的异常（Genuine Anomalies）： 确实是异常值，模型不应该学习。
尚未学到的可泛化模式（Unlearned but Generalizable Patterns）： 模型目前能力不足导致的误差，但在训练中应该继续学习。
挑战： 需要一种机制来区分这两种高残差的时间步。
偏差度量的引入
为解决上述挑战，论文引入了 偏差（Deviation）度量($S(mathbf{X}_t)$)，其核心灵感是比较当前残差与理论残差下界：
($S(mathbf{X}_t) = |mathbf{X}_t – f(mathbf{X}; heta)_t)| – epsilon^{ ext{LB}}_t quad ext{(12)}$)
是模型 f 的当前残差 ($|epsilon_t|$)。
是残差的理论下界（Theoretical Lower Bound）。
关键分离机制
真正的异常时间步： 由于Ground Truth发生偏差，理论上最小的预测误差 也会较高。因此，即使当前残差 很大，其与高下界 之间的差值 ($S(mathbf{X}_t)$)仍然会相对较小。
尚未学到的时间步（可泛化）： 这些点虽然当前残差 ($|epsilon_t|$) 很大，但其理论上是可以被一个理想模型准确预测的（即 较小）。因此，当前残差与较小的下界之间的差值 (S(mathbf{X}_t)) 会较大。
结论：($S(mathbf{X}_t)$)越小，越可能是真正的、不可泛化的异常点。
实践中的偏差估计
在实践中，残差理论下界 是无法直接获得的，需要进行估计：
估计下界 ($hat{epsilon}^{ ext{LB}}_t$)： 通过训练一个轻量级模型 
（通常在整个训练集 (mathcal{D}_{ ext{train}}) 上训练）来获得。这个轻量级模型的残差被视为残差的下界估计。
异常掩码的生成
与不确定性掩码类似，异常掩码 通过硬阈值 
策略生成：
阈值 (gamma_a)： 过滤掉顶部 
具有最小 (hat{S}(mathbf{X}_t))的时间步。
掩码规则：
结果： 被标记为 0 的时间步被认为是真正的异常，将被排除在损失计算之外，防止模型学习特定于实例的偏差。
动态掩码的优势
方法采用动态掩码（Dynamic Masking），即掩码是根据当前模型的预测 动态调整的，这带来了两个关键优势：
减轻偏差： 相比于在训练前就确定不变的静态掩码，动态掩码可以适应训练过程，从而减轻对训练数据分布引入的偏差。
处理极端事件： 对于稀有但关键的极端事件，动态掩码允许模型先学习最可泛化的模式，然后逐步尝试学习先前被认为是异常的极端时间步。
实验
实验设置
数据集 (Datasets)
实验使用了 8 个真实的公开数据集，这些数据集是 TSF 任务中常用的基准：
常规数据集： Electricity (电力消耗), Exchange (汇率), Weather (天气), ILI (流感样疾病)。
ETT 数据集： ETTh1, ETTh2, ETTm1, ETTm2 (电力变压器数据)。
基线模型 (Baselines)
选择性学习策略被用于增强六个主流的深度 TSF 模型的性能，这些模型涵盖了不同的网络架构：
基于 Transformer 的模型： Informer, Crossformer, PatchTST, iTransformer。
基于 CNN 的模型： TimesNet。
基于 MLP 的模型： TimeMixer。
估计模型 (Estimation Model)
在选择性学习的异常掩码构建中，需要一个轻量级模型 来估计残差下界。
选定模型： 论文统一选择 DLinear 作为所有基线模型的残差下界估计模型。
实验参数设置 (Experimental Settings)
预测窗口长度 (F)：
ILI 数据集：($F in {24, 36, 48, 60}$)。
其他数据集：
。
回顾窗口长度 ( L )： 通过搜索最佳结果来确定。
超参数调整： 在将 SL 应用于基线模型时，保持基线模型的原始超参数设置不变，仅调整选择性学习的两个掩码比率 ($r_a$) 和 
，以确保公平评估。
优化器： 使用 Adam 优化器。
评估指标 (Metrics)
MAE 和 MSE
主要结果 (Main Results)
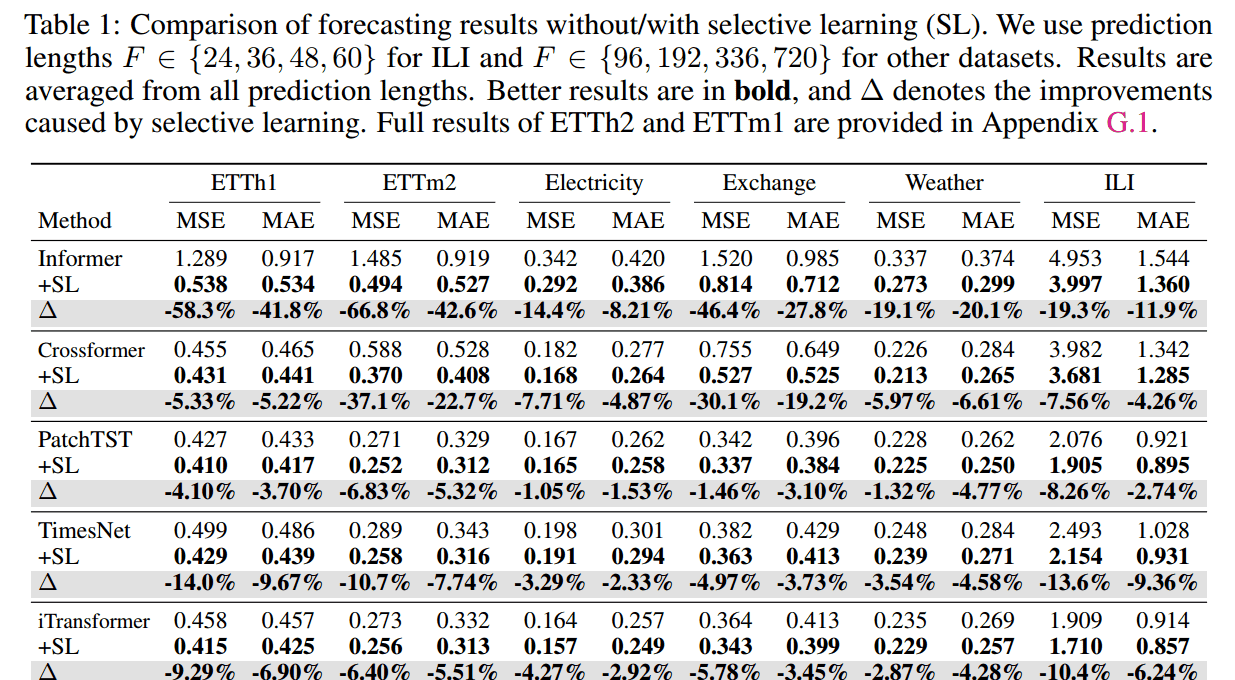
一致性提升： 在所有 8 个数据集和所有预测长度的组合中，SL 始终增强了模型的性能（在所有 192 个测试案例中）。
对早期架构的巨大影响： SL 对容易过拟合的早期架构效果尤为显著。
Informer： 平均 MSE 降低 37.4%，MAE 降低 25.4%。在 ETTm2 数据集上，MSE 甚至降低了 66.8%。
Crossformer： 平均 MSE 降低 15.6%，MAE 降低 10.5%。
对 SOTA 模型的持续增益： 即使对于最新的 SOTA（State-of-the-Art）基线模型，SL 仍能带来额外增益。
iTransformer： 平均 MSE 降低 6.5%，MAE 降低 4.4%。
TimeMixer： 平均 MSE 降低 4.3%，MAE 降低 3.3%。
超越现有技术： 即使在模型已经使用了 RevIN 等现有的分布偏移缓解技术（Distribution Shift Mitigation Techniques）的情况下，SL 依然有效，这证实了它提供了额外的性能提升。
零样本预测 (Zero-shot Forecasting)
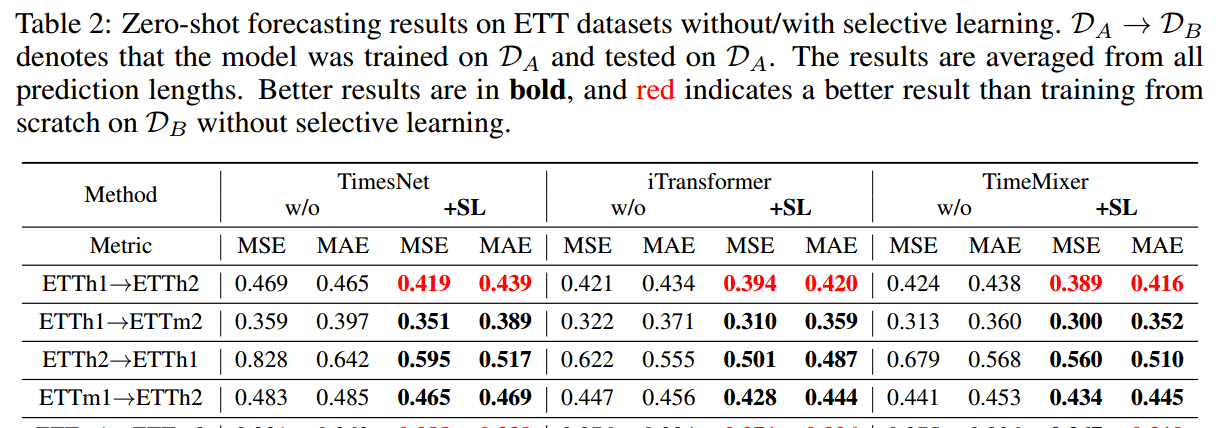
泛化优势： SL 持续增强了基线模型在零样本预测场景中的性能，证明了其更强的泛化能力。
挑战场景显著提升： 在具有挑战性的泛化场景（如 ETTh2→ETTh1 和 ETTm2→ETTm1）中，SL 带来了显著改进，平均 MSE 降低 22.6%，MAE 降低 14.5%。
表现优于从头训练： 在某些情况下（如 ETTh1→ETTh2 和 ETTm1→ETTm2），使用 SL 训练的模型在目标数据集上的表现甚至优于直接在目标数据集上从头开始训练的模型，进一步强调了 SL 带来的泛化优势。
Comparison with Other Training Objectives
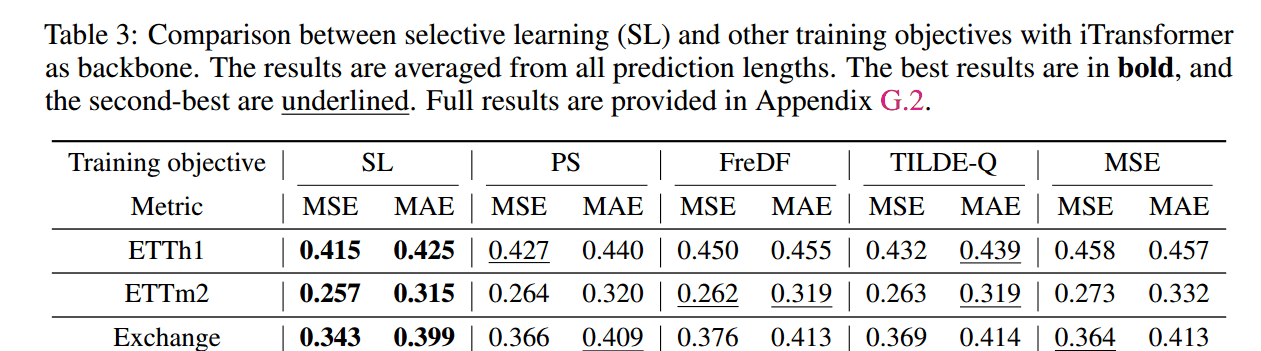
对比目标： 形状损失（shape-based，如 TILDE-Q）、频率损失（frequency-based，如 FreDF）和分布损失（distribution-based，如 PS loss）。
结果： SL 策略始终获得更优的性能。
结论： 实验结果验证了通过全局对齐（无论是基于形状、分布，还是在时域或频域）来训练模型是次优的（suboptimal），而 SL 的选择性、逐点优化方法更有效。
Ablation Study and Hyperparameter Analysis
A. 消融研究 (Ablation Study)
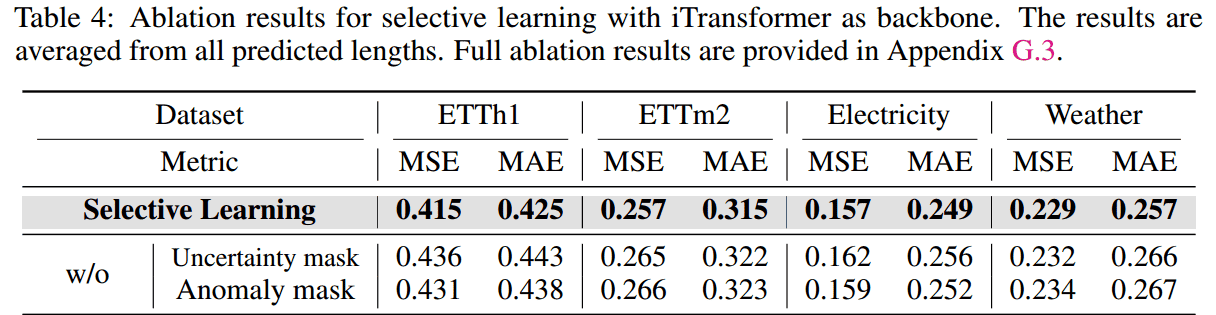
双重掩码的必要性： 去除不确定性掩码或异常掩码都会导致显著的性能下降，表明这两个掩码都提供了必要且独特的功能，共同过滤非可泛化模式。
随机掩码无效： 将双重掩码机制替换为相同掩码比率的随机掩码，模型的性能与未掩码的基线模型相当甚至更差。
结论： SL 的有效性根本上源于其双重掩码机制能够定向选择可泛化时间步，而不仅仅是随机地选择子集。
B. 掩码比率的影响 (Effects of Masking Ratio)
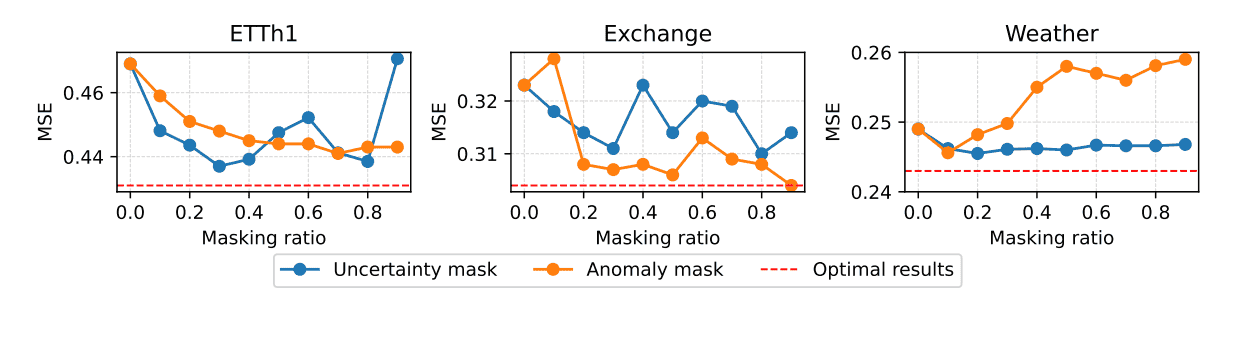
高非平稳性数据集（Non-stationary）： 像 ETTh1 和 Exchange 这种具有高度非平稳性的数据集，更大的掩码比率（即过滤更多的点）能带来更好的性能，这表明这些数据集存在严重的过拟合，模型需要高度专注于最可泛化的模式。
周期性数据集（Periodic）： 具有周期性模式的数据集（如 Weather），使用较小的掩码比率即可获得性能提升。
特殊情况： 在 Exchange 数据集上，90% 的异常掩码比率达到了峰值性能，表明市场异常值对该数据集的影响远大于噪声。
C.估计模型的影响 (Effects of Estimation Model)
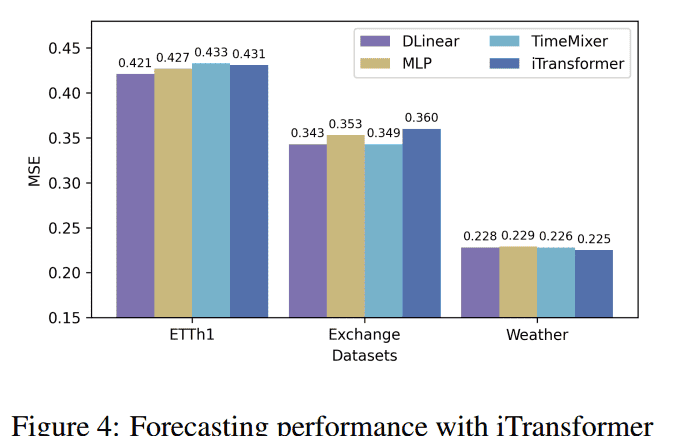
调查内容： 探究用于估计残差下界（异常掩码所需）的轻量级模型对整体性能的影响，对比了 DLinear、MLP、TimeMixer 和 iTransformer。
发现：
对于高非平稳性数据集（ETTh1 和 Exchange），更简单的估计模型表现更好。
对于具有周期性模式的数据集（Weather），更复杂的估计模型有益。
结论： 尽管存在这些趋势，但估计模型的选择对整体性能影响有限，强调 SL 策略的鲁棒性。
学习曲线分析 (Learning Curve Analysis)
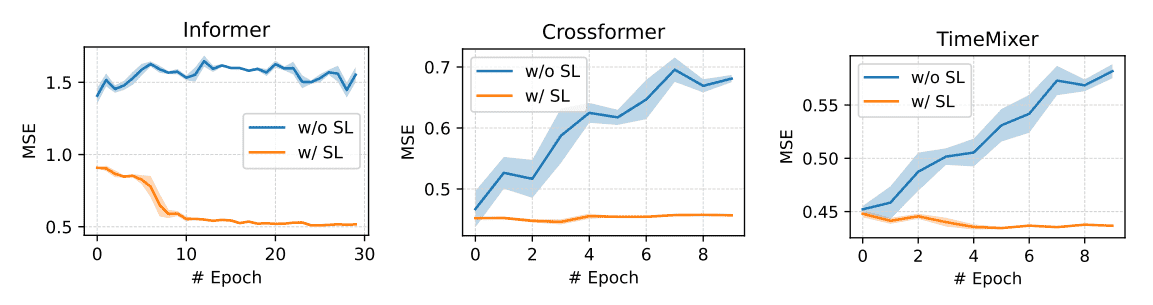
验证： 通过在 ETTh1 数据集上展示学习曲线，进一步验证了 SL 缓解过拟合的能力。
效果： 尽管所有基线模型都表现出不同程度的过拟合，但经过 SL 训练的模型都实现了稳定的收敛和更优的性能。
© 版权声明
文章版权归作者所有，未经允许请勿转载。
相关文章
暂无评论...