高中数学函数核心100术语

高中数学中与函数相关的100个核心术语。按照知识的逻辑体系进行了分类，方便系统性地理解和复习。掌握这些术语，就等于掌握了函数章节的骨架。

一、 函数的基本概念

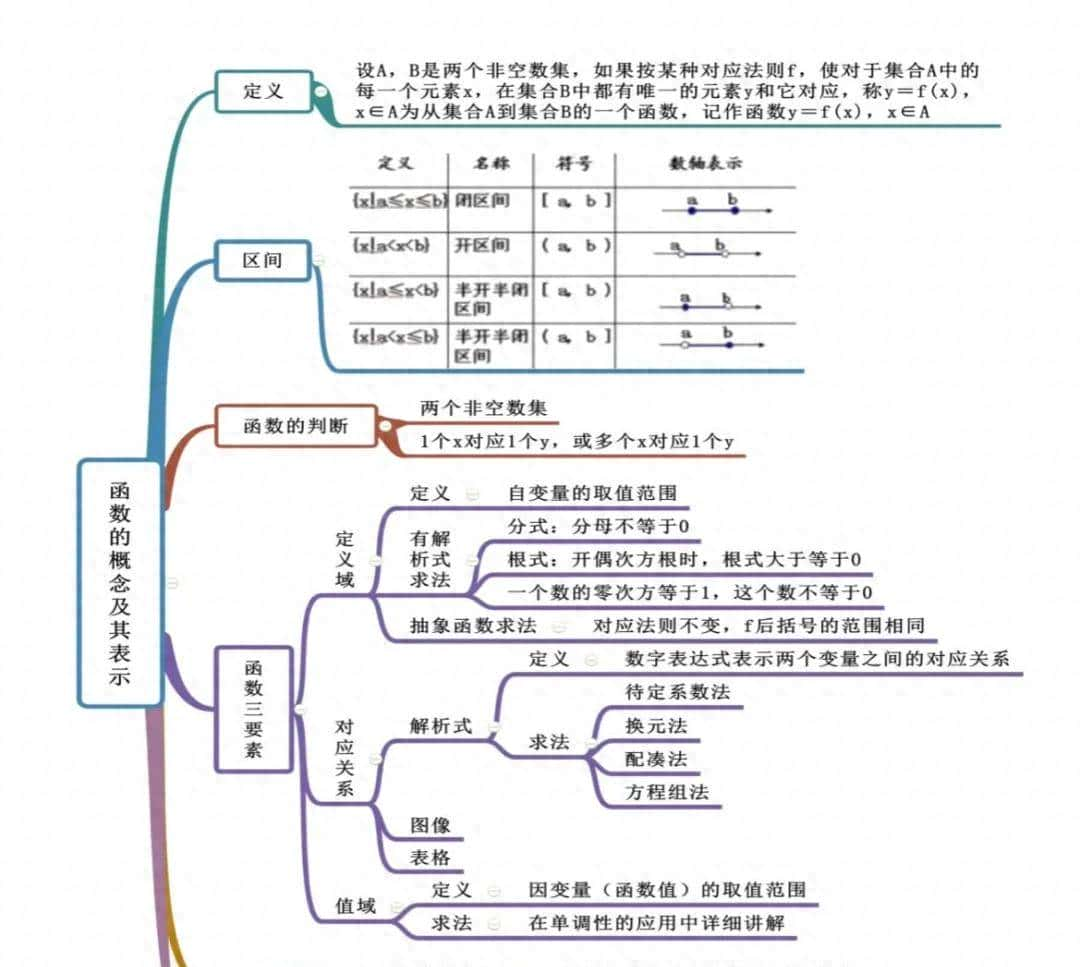
1. 函数：一种特殊的对应关系，每个自变量都有唯一的因变量与之对应。
2. 自变量：主动变化的量，一般用 x 表明。
3. 因变量：随自变量变化而变化的量，一般用 y 表明。
4. 定义域：自变量 x 的取值范围。
5. 值域：因变量 y 的取值范围。
6. 对应关系：定义域到值域的映射法则，即 f 。
7. 函数值：对于定义域内某个具体值 x_0 ，对应的 y_0 = f(x_0) 。
8. 区间：表明实数范围的常用方法（如开区间、闭区间）。
9. 开区间：不包含端点的区间，记作 (a, b) 。
10. 闭区间：包含端点的区间，记作 [a, b] 。
11. 半开半闭区间：包含一个端点，记作 [a, b) 或 (a, b] 。
12. 无穷区间：包含无穷大的区间，如 [a, +infty) 。
13. 函数的三要素：定义域、对应关系、值域。两个函数相等的充要条件是三要素一样。
14. 映射：两个集合元素之间的对应关系。函数是数集到数集的映射。
15. 象和原象：在映射 f: A o B 中，与 a in A 对应的 b in B 叫做 a 的象， a 叫做 b 的原象。

二、 函数的表明与性质

16. 解析法：用数学表达式表明函数。
17. 列表法：用表格列出函数值。
18. 图像法：在坐标系中用曲线表明函数。
19. 函数图像：所有点 (x, f(x)) 构成的集合。
20. 单调性：函数在区间上的增减性质。
21. 增函数：当 x_1 < x_2 时，有 f(x_1) < f(x_2) 。
22. 减函数：当 x_1 < x_2 时，有 f(x_1) > f(x_2) 。
23. 单调区间：函数具有单调性的区间。
24. 奇偶性：函数图像关于原点或y轴的对称性。
25. 奇函数：满足 f(-x) = -f(x) ，图像关于原点对称。
26. 偶函数：满足 f(-x) = f(x) ，图像关于y轴对称。
27. 周期性：存在非零常数 T ，使得 f(x+T) = f(x) 对定义域内任意 x 都成立。
28. 周期：使函数值重复的最小正数 T （最小正周期）。
29. 对称性：函数图像的轴对称或中心对称性质。
30. 有界性：存在正数 M ，使得 |f(x)| leq M 对所有 x 成立。
31. 最大值：函数在定义域或其区间上的最大函数值。
32. 最小值：函数在定义域或其区间上的最小函数值。
33. 极值点：函数在该点的值比邻近点都大或都小。
34. 零点：使 f(x) = 0 的实数 x 。
35. 交点：函数图像与坐标轴或其他图像的交点。

三、 基本初等函数（一）

37. 一次函数：形如 y = kx + b ( k
    eq 0 ) 的函数。
38. 斜率：一次函数 y=kx+b 中的 k ，表明直线的倾斜程度。
39. 截距：直线与坐标轴的交点坐标（如y轴截距为 b ）。
40. 正比例函数：特殊的一次函数，形如 y = kx ( b=0 )。
41. 二次函数：形如 y = ax^2 + bx + c ( a
    eq 0 ) 的函数。
42. 抛物线：二次函数的图像。
43. 开口方向：由二次项系数 a 的正负决定（ a>0 向上， a<0 向下）。
44. 顶点：抛物线的最高点或最低点。
45. 对称轴：过顶点且垂直于x轴的直线，方程为 x = -frac{b}{2a} 。
46. 判别式： Delta = b^2 – 4ac ，用于判断一元二次方程根的情况。

四、 基本初等函数（二）：幂、指、对函数

48. 反比例函数：形如 y = frac{k}{x} ( k
    eq 0 ) 的函数。
49. 幂函数：形如 y = x^a ( a 为常数）的函数。
50. 指数函数：形如 y = a^x ( a>0 且 a
    eq 1 ) 的函数。
51. 底数：指数函数 y=a^x 中的 a 。
52. 指数：幂运算 a^x 中的 x 。
53. 对数函数：形如 y = log_a x ( a>0 且 a
    eq 1 ) 的函数。
54. 真数：对数函数 y=log_a x 中的 x ( x>0 )。
55. 常用对数：以10为底的对数，记作 lg x 。
56. 自然对数：以自然常数 e 为底的对数，记作 ln x 。
57. 指数式与对数式的互化： a^b = N Leftrightarrow log_a N = b 。
58. 对数恒等式：如 a^{log_a N} = N 。

五、 函数的运算与变换

59. 复合函数：函数套函数，如 y = f(g(x)) 。
60. 内层函数：复合函数 f(g(x)) 中的 g(x) 。
61. 外层函数：复合函数 f(g(x)) 中的 f(u) 。
62. 四则运算：函数间的加、减、乘、除（分母不为零）。
63. 平移变换： 左加右减： y = f(x+h) 是 y=f(x) 图像向左 ( h>0 ) 或向右 ( h<0 ) 平移 |h| 个单位。 上加下减： y = f(x) + k 是 y=f(x) 图像向上 ( k>0 ) 或向下 ( k<0 ) 平移 |k| 个单位。
64. 对称变换： y = -f(x) ：关于x轴对称。 y = f(-x) ：关于y轴对称。 y = -f(-x) ：关于原点对称。
65. 翻折变换： y = |f(x)| ：将 f(x) 图像在x轴下方的部分翻折到x轴上方。 y = f(|x|) ：去掉 f(x) 图像在y轴左侧的部分，并将右侧部分对称到左侧。
66. 伸缩变换： 纵向伸缩： y = Af(x) ( A>1 伸长， 0<A<1 压缩)。 横向伸缩： y = f(omega x) ( omega>1 压缩， 0<omega<1 伸长)。

六、 函数的应用与拓展

67. 分段函数：在不同定义域区间上用不同解析式表明的函数。
68. 绝对值函数：如 y = |x| 。
69. 最值问题：求函数的最大值或最小值。
70. 恒成立问题：如 f(x) > 0 在区间上恒成立。
71. 存在性问题：存在某个 x 使得 f(x) 满足某种条件。
72. 根的分布：研究一元二次方程根相对于某数的位置。
73. 函数方程：含有未知函数的方程。
74. 抽象函数：未给出具体解析式，只给出运算性质的函数。
75. 定义法：证明函数单调性的基本方法（作差、变形、判号）。
76. 赋值法：解抽象函数问题的常用技巧。
77. 反函数：将原函数的自变量与因变量互换得到的函数，记作 y = f^{-1}(x) 。
78. 原函数与反函数的图像关于直线 y=x 对称。
79. 函数模型：描述现实问题的数学模型。
80. 线性增长：一次函数模型。
81. 指数增长：指数函数模型。
82. 对数增长：对数函数模型。
83. 幂函数增长：幂函数模型。
84. 函数拟合：根据数据选择适当的函数模型。

七、 高阶概念与思想方法

85. 导数：函数在某一点处的瞬时变化率。
86. 切线：导数在几何上表明函数曲线在某点的切线斜率。
87. 单调性的导数判定法：用导数的正负判断函数的单调性。
88. 极值的导数判定法：利用导数求函数的极值点。
89. 连续：函数图像不断开。
90. 间断：函数图像断开。
91. 渐近线：函数图像无限逼近的直线（如水平、垂直、斜渐近线）。
92. 凸凹性（或称函数的凹凸性）：函数图像的弯曲方向。
93. 拐点：函数凸凹性改变的点。
94. 参数方程：用参数 t 表明 x 和 y 的关系。
95. 隐函数：变量 x, y 之间的关系由方程 F(x, y)=0 确定。
96. 迭代：反复将函数的输出作为输入的过程 x_{n+1} = f(x_n) 。
97. 不动点：满足 f(x) = x 的点。
98. 数形结合：将代数问题与几何图形相结合的思想方法。
99. 分类讨论：根据参数范围或情况不同分别进行讨论的思想方法。

使用提议：

• 查漏补缺：将此列表作为检查清单，标记出你不熟悉或理解模糊的术语。
• 概念关联：学习时不要孤立记忆，要理解术语之间的逻辑联系（例如，奇偶性与对称性的关系）。
• 回归实例：对每个术语，都要找到对应的函数解析式或图像例子，加深理解。

希望这份详尽的术语汇总能对你的高中数学学习有极大的协助！

#晒图笔记大赛#​